Module 6 Demonstration

class: center, middle, inverse, title-slide

.title[
# Module 6 Demonstration
]
.subtitle[
## Scan: Outliers
]

---

# Outliers

- In statistics, an outlier is defined as **an observation which stands far away from the most of the other observations**.

- An outlier deviates so much from other observations as to arouse suspicion that was generated by a different mechanism (Hawkins 1980).

---

# Types of Outliers

- Outlier can be **univariate** and **multivariate**.

- **Univariate outliers** can be found when looking at a distribution of values in a single variable.

- **Multivariate outliers** can be found in a n-dimensional space (of n-variables). In order to find them, we need to look at distributions in multi-dimensions.

---

# Class Activity:

- Work in small groups.

- Have a look at the next four data examples with visualizations.

- Inspect the variables **visually** for possible univariate and multivariate outliers.

---

# Data Set 1: Age distribution

- Are there any outliers?

``` r
df1 <- c(34, 30, 30, 29, 67, 29, 27, 30, 31, 31, 28)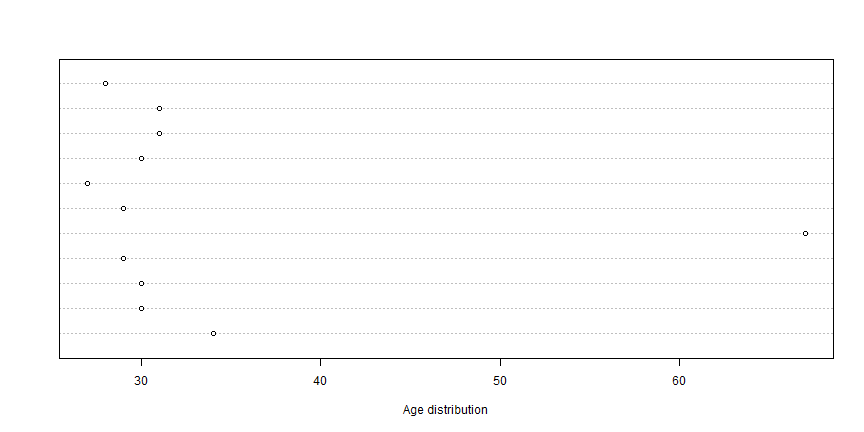
```

???

Age = 67 is a possible (univariate) outlier

---

# Data set 2: Anscombe's data

- Four x-y datasets which have the same traditional statistical properties (mean, variance, correlation, regression line, etc.), yet are quite different (read more [here](https://en.wikipedia.org/wiki/Anscombe%27s_quartet)).

``` r
anscombe1<- anscombe[, c(3,7)]
anscombe1
```

```
##    x3    y3
## 1  10  7.46
## 2   8  6.77
## 3  13 12.74
## 4   9  7.11
## 5  11  7.81
## 6  14  8.84
## 7   6  6.08
## 8   4  5.39
## 9  12  8.15
## 10  7  6.42
## 11  5  5.73
```

---

# Data set 2:  Anscombe's data Cont.

- Are there any outliers?

---

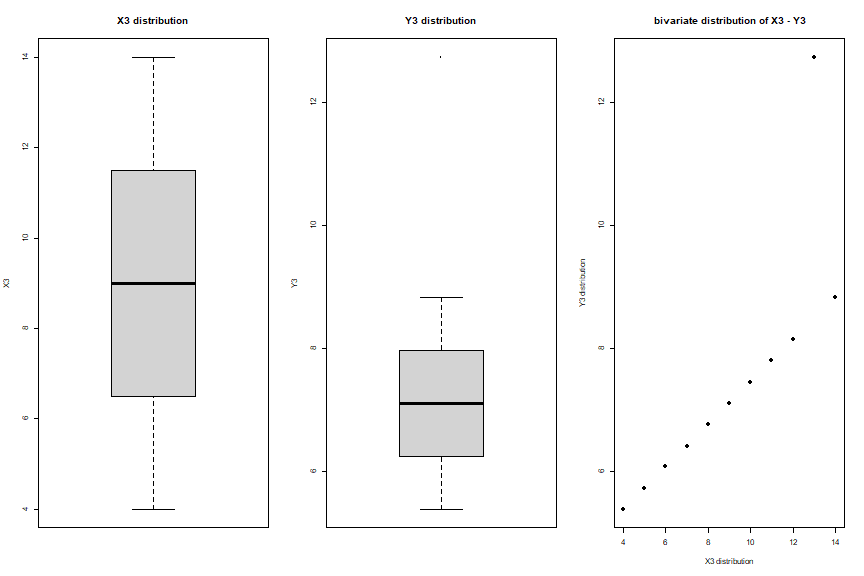
# Data set 3: Anscombe's data

- Now let's take another pair (X4-Y4) in the anscombe data set.

``` r
anscombe2<- anscombe[, c(4,8)]
anscombe2
```

```
##    x4    y4
## 1   8  6.58
## 2   8  5.76
## 3   8  7.71
## 4   8  8.84
## 5   8  8.47
## 6   8  7.04
## 7   8  5.25
## 8  19 12.50
## 9   8  5.56
## 10  8  7.91
## 11  8  6.89
```

---

# Data set 3:  Anscombe's data Cont.

- Are there any outliers?

---

# Data Set 4: Height and Weight distribution

- Are there any outliers?

???

- When we look at the univariate distributions of Height and Weight (i.e., using box plots) separately, we don't spot any abnormal cases (i.e. above and below the `$1.5\times IQR$` fence).

- However, when we look at the bivariate (two dimensional) distribution of Height and Weight (using a scatter plot), we can see that we have one observation whose weight is 45.19 kg and height is 185.09 (on the upper-left side of the scatter plot).

- This observation is far away from the most of the other weight and height combinations thus, will be seen as a multivariate outlier.

---

# Most Common Causes of Outliers

- Some common causes of outliers (taken from: https://www.analyticsvidhya.com/blog/2016/01/guide-data-exploration/)

- **Data Entry Error:** Outliers due to the human errors during data collection, recording, or entry. 
      - **Measurement Error:** The most common source of outliers. Measurement instrument used turns out to be faulty.
      - **Experimental Error:** Experimental errors during data extraction, experiment/survey planning and executing.
      - **Intentional Error:** Commonly is found in self-reported measures that involves sensitive data. 
      - **Data Processing Errors:** It is possible that some manipulation or extraction errors may lead to outliers in the data set.
      - **Sampling Error:** Sometimes, outliers can arise due to the sampling process. Typically because of few observations in a sample.

---

# Why Outliers are problematic?

- Outliers can drastically change the results of the data analysis and statistical modeling. Some unfavorable impacts of outliers are:

- increasing the error variance; 
    - reducing the power of statistical tests; 
    - influencing the estimates of model parameters that may be of substantive interest.

- Therefore, identifying and properly handling these values are crucial.

---

# Detecting Outliers

- There are many methods for detecting outlier(s).

- Majority of them deal with numerical data.

- We will look at the most basic descriptive, graphical and distance based methods to detect outliers with their application using R packages.

- **Univariate Outlier Detection Methods**
          - Tukey
          - Box plots
          - z-score 
      - **Multivariate Outlier Detection Methods**
          - Scatter plots
          - Mahalanobis distance

---

# Univariate Outlier Detection Methods

- As seen in the examples, the simplest method for detecting univariate outliers is the use of **box plots**.

- A box plot is a graphical display for describing the distribution of the data using the median, the first (Q1) and third quartiles (Q3), and the *inter-quartile range* (IQR = `$Q3-Q1$`).

- Below is an illustration of a typical box plot

---

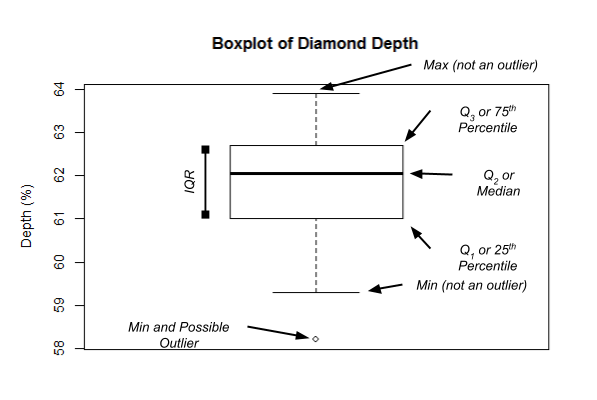
# Univariate Outlier Detection Methods Cont.

- "**Tukey’s method of outlier detection**" is used to detect outliers in the box plots.

- This method (nonparametric) is mainly used to test outliers in non-symmetric/ non-normal data distributions.

- Outliers are defined as the values in the data set that fall beyond the range of `$Q1 -1.5 \times IQR$` to `$Q3 + 1.5 \times IQR$`.

- These limits are called "**outlier fences**" and any values outside the outlier fences are presented using an "o" or "*" on the box plot.

- The `boxplot()` function uses this technique to detect possible outliers.

---

# Class Activity: Your turn!

The cars data set (from datasets package) includes the speed of cars and the distances taken to stop. Note that the data were recorded in the 1920s.

``` r
library(datasets)
head(cars)
```

```
##   speed dist
## 1     4    2
## 2     4   10
## 3     7    4
## 4     7   22
## 5     8   16
## 6     9   10
```

- Task 1: Identify the possible outliers for `speed` using the box plot and Tukey’s method.

- Task 2: Identify the possible outliers for `dist` using the box plot and Tukey’s method.

- Task 3: Identify the location of outlier(s) in `dist`.

???

``` r
# Task 1:

cars$speed %>%  boxplot(main="Box Plot of speed", ylab="Speed in km/h", col = "grey")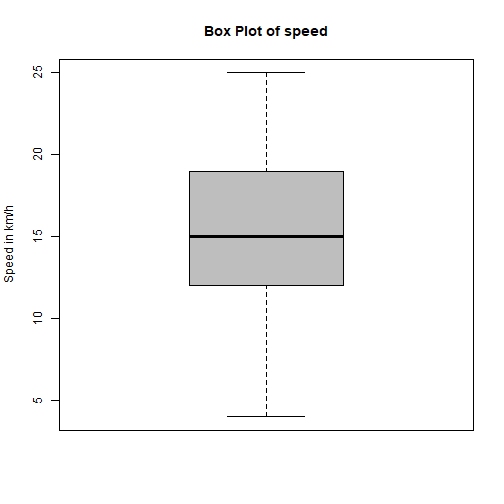
```

``` r
# Task 2:

cars$dist %>%  boxplot(main="Box Plot of stopping distance", ylab="Stopping distance in meters", col = "grey")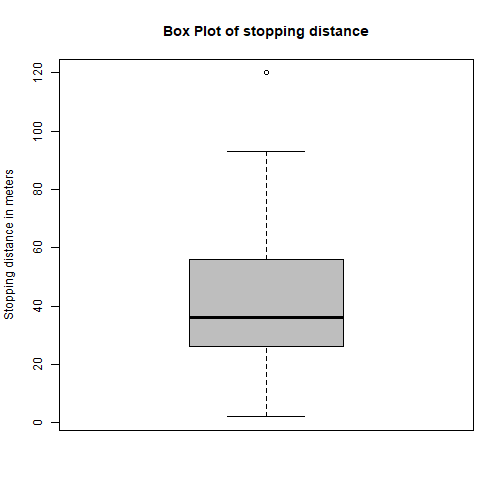
```

``` r
# Task 3:

# Option 1:

cars_outliers <- cars$dist %>%  boxplot(main="Box Plot of stopping distance", ylab="Stopping distance in meters", col = "grey")

# The `out` value will report the values of any data points which lie beyond the outlier fences.

cars_outliers$out
```

```
## [1] 120
```

``` r
# Then we can find the location of that value using basic subsetting

cars[(cars$dist == 120),]
```

```
##    speed dist
## 49    24  120
```

``` r
# Other options

# The package car identifies the outliers on the boxplot

library(car)
```

```
## Warning: package 'car' was built under R version 4.4.3
```

```
## Loading required package: carData
```

```
## 
## Attaching package: 'car'
```

```
## The following object is masked from 'package:dplyr':
## 
##     recode
```

``` r
Boxplot(cars$dist, id=TRUE)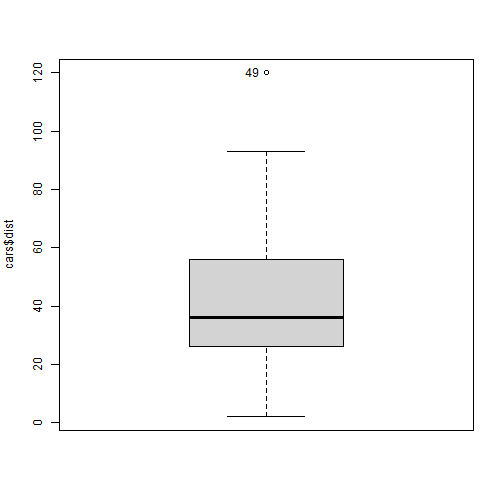
```

```
## [1] 49
```

- According to the second box plot, there is one suggested outlier for the stopping distance which is 120 km/h and it is the 49th observation in the data set.

---

# Univariate Outlier Detection Methods Cont.

- There are also distance based methods to detect univariate outliers. One of them is to use the `$z$`-scores (i.e., normal scores) method.

- In this method, a standardized score (z-score) of all observations are calculated using the following equation:

$$ z_i = \frac{X_i - \bar{X}}{S}$$

- Here `$X_i$` denotes the values of observations, `$\bar{X}$` and `$S$` are the sample mean and standard deviation, respectively.

- An observation is regarded as an outlier based on its `$z$`-score, if the absolute value of its **z-score is greater than 3**.

- This method assumes that the underlying data is normally distributed. **Therefore, if the distribution is not approximately normal, this method shouldn't be used.**

- The "**outliers package**" provides a number of useful functions to systematically extract outliers. Among those, the `scores()` function will calculate the `$z$`-scores for a given vector.

---

# Class Activity: Your turn!

Use the `scores` function in `outliers` package to identify the outliers with z-score approach.

- Task 1: Identify the possible outliers for `speed`. If there exists an outlier, identify its location.

- Task 2: Identify the possible outliers for `dist`. If there exists an outlier, identify its location.

???

``` r
# Task 1:
library(outliers)

z_speed <- cars$speed %>%  scores(type = "z") 
which( abs(z_speed) >3 )
```

```
## integer(0)
```

``` r
# Task 2:

z_dist <- cars$dist %>%  scores(type = "z") 
which( abs(z_dist) >3 )
```

```
## integer(0)
```

``` r
boxplot(cars$dist)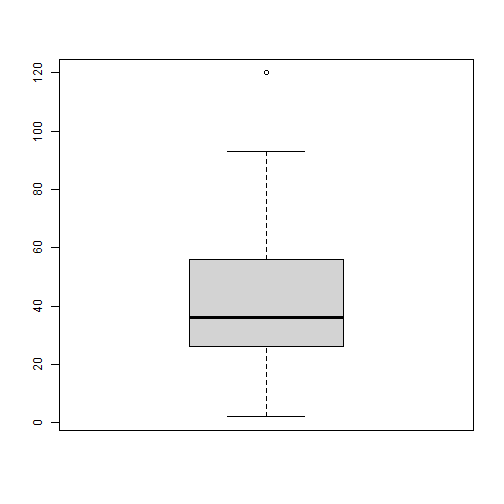
```

---
# Class Activity: Cont.

``` r
library(ggplot2)
library(nortest)
data <- cbind(cars$speed,cars$dist)

shapiro_test <- shapiro.test(data)
print(shapiro_test)
```

```
## 
## 	Shapiro-Wilk normality test
## 
## data:  data
## W = 0.8234, p-value = 1.386e-09
```

``` r
#a p-value less than 0.05 indicates that the data is not normally distributed
```

---

# Multivariate Outlier Detection Methods

- When we have only **two variables**, the bivariate visualisation techniques like bivariate scatter plots and box plots, can easily be used to detect any outliers.

- Scatter plots are used to visualise the relationship between two quantitative variables (x, y).

- They are also very useful tools to detect obvious outliers for the two dimensional data (i.e., for two continuous variables).

- The `plot()` function will be used to get the scatter plot and detect outliers visually.

``` r
plot(y, x)
```

---

# Multivariate Outlier Detection Methods Cont.

- When we have one factor (categorical) variable and one continuous variable, bivariate box plot can be used to detect outliers for the continuous variable in each level of the factor variable.

- To get a bivariate box plot with one factor variable (x) and a numerical variable (y) we can again use the `boxplot()` function with the following generic arguments:

``` r
boxplot(y ~ x)
```

---

# Class Activity: Your turn!

Use the cars data set (from datasets package).

``` r
library(datasets)
head(cars)
```

```
##   speed dist
## 1     4    2
## 2     4   10
## 3     7    4
## 4     7   22
## 5     8   16
## 6     9   10
```

- Task 1: Inspect the data for possible multivariate outliers using scatter plot.

- Task 2: Split the `speed` variable into two groups and name this variable as `speed_group`. The first group should include speed `$\le$` 15km/h and the second should include speed `$>$` 15km/h.

- Task 3: Inspect the possible outliers in `dist` grouped by `speed_group`.

???

``` r
#Task 1:

plot(cars$speed, cars$dist)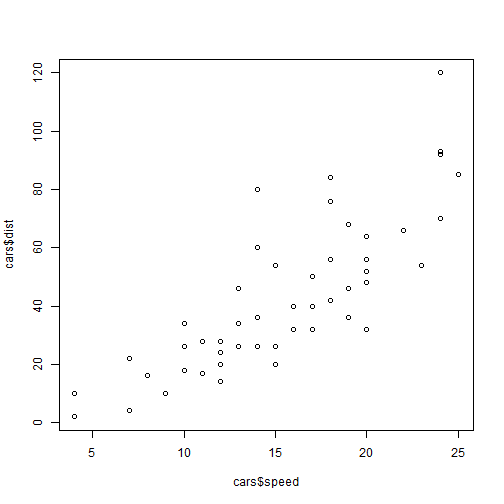
```

``` r
# Task 2:

cars <- mutate(cars, speed_group = ifelse( (speed > 15), 2, 1))
cars$speed_group <- factor(cars$speed_group, labels=c("=<15", ">15"))

# Task 3:

boxplot(cars$dist ~ cars$speed_group)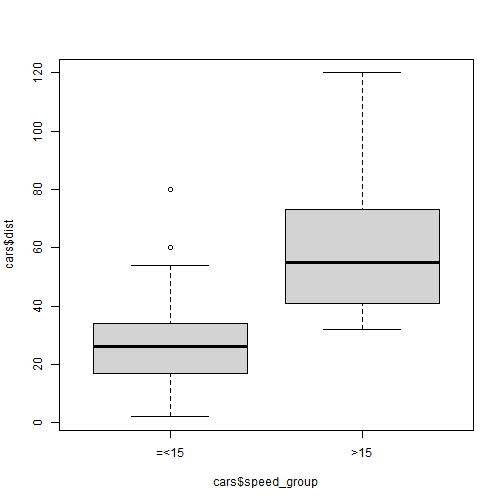
```

---

# Multivariate Outlier Detection Methods Cont.

- When there are more >2 variables, scatter plots can no longer be used. For such cases, multivariate distance based methods of outlier detection can be used.

- **The Mahalanobis distance** is the most commonly used distance metric to detect outliers for the multivariate setting.

- This distance is simply an extension of the univariate `$z$`-score, which also accounts for the correlation structure between all the variables.

- Mahalanobis distance follows a Chi-square distribution with n (number of variables) degrees of freedom, therefore **any Mahalanobis distance greater than the critical chi-square value is treated as outliers**.

- We will use the `mvn()` function from `MVN` package to get these distances as it will also provide us the useful Mahalanobis distance vs. Chi-square quantile distribution plot (QQ plot).

---

# Multivariate Outlier Detection Methods Cont.

- The `mvn()` function lets us to define the multivariate outlier detection method using the `multivariateOutlierMethod` argument.

``` r
results <- mvn(data = .., multivariateOutlierMethod = "quan", showOutliers = TRUE)
```

- When we use `multivariateOutlierMethod = "quan"` argument, it detects the multivariate outliers using the chi-square distribution critical value approach mentioned before.

- The `showOutliers = TRUE` argument will depict any multivariate outliers and show them on the QQ plot.

---

# Class Activity: Your turn!

Use the cars data set (from datasets package).

``` r
library(datasets)
head(cars)
```

```
##   speed dist speed_group
## 1     4    2        =<15
## 2     4   10        =<15
## 3     7    4        =<15
## 4     7   22        =<15
## 5     8   16        =<15
## 6     9   10        =<15
```

- Task 1: Inspect the data for possible multivariate outliers using the Mahalanobis distance vs. Chi-square quantile distribution plot.

- Task 2: Find the locations of the multivariate outliers.

???

``` r
#Task 1:

results <- mvn(data = cars[,1:2], multivariateOutlierMethod = "quan", showOutliers = TRUE)
```

``` r
# Task 2:

results$multivariateOutliers
```

```
##    Observation Mahalanobis Distance Outlier
## 49          49               36.565    TRUE
## 23          23               24.263    TRUE
## 35          35               16.337    TRUE
## 48          48               11.718    TRUE
## 47          47               11.113    TRUE
## 34          34               10.288    TRUE
## 22          22                7.887    TRUE
```

---

# Approaches to Handling Outliers

- Most of the ways to deal with outliers are similar to the methods of missing values like:

- deleting 
    - imputing  (i.e., mean, median, mode) 
    
- There are also other approaches specific to dealing with outliers like:

- capping 
    - transforming* 
    - binning*

*Transforming and binning will be covered in the next module (Module 7: Transform).

---

# Excluding or Deleting Outliers

- Some authors recommend that if the outlier is due to data entry error, data processing error or outlier observations are very small in numbers, then leaving out or deleting the outliers would be used as a strategy.

- When this is the case, we can exclude/delete outliers using the basic filtering and subsetting functions in combination with `which()`.

---

# Imputing

- Like imputation of missing values, we can also impute outliers.

- We can use mean or median imputation methods to replace outliers.

- Before imputing values, always check whether the outlier is a result of data entry/processing error.

- If the outlier is due to a data entry/processing error, then go with imputing.

---

# Capping (a.k.a Winsorising)

- Capping or winsorising involves replacing the outliers with the nearest neighbors that are not outliers.

- Outliers that lie outside the outlier fences are capped by replacing those observations outside LL with the value of 5th percentile and those that lie above UL with the value of 95th percentile.

---

# Capping (a.k.a Winsorising) Cont.

- In order to cap the outliers we can use a user-defined function as follows (taken from: [Stackoverflow](https://stackoverflow.com/questions/13339685/how-to-replace-outliers-with-the-5th-and-95th-percentile-values-in-r?utm_medium=organic&utm_source=google_rich_qa&utm_campaign=google_rich_qa)):

``` r
# Define a function to cap the values outside the limits

cap <- function(x){
    quantiles <- quantile( x, c(.05, 0.25, 0.75, .95 ) )
    x[ x < quantiles[2] - 1.5*IQR(x) ] <- quantiles[1]
    x[ x > quantiles[3] + 1.5*IQR(x) ] <- quantiles[4]
    x
}
```

---

# Class Activity: Your turn!

Use x3-y3 pair in anscombe data set:

``` r
anscombe1<- anscombe[, c(3,7)]
anscombe1
```

```
##    x3    y3
## 1  10  7.46
## 2   8  6.77
## 3  13 12.74
## 4   9  7.11
## 5  11  7.81
## 6  14  8.84
## 7   6  6.08
## 8   4  5.39
## 9  12  8.15
## 10  7  6.42
## 11  5  5.73
```

- Task 1: For `y3`, cap the outlier using the function given before.

- Task 2: For `y3`, replace the outlier with its median.

???

``` r
# Task 1:

task1 <- anscombe1$y3 %>% cap()

# Task 2: Similar to task 1, we can write our own function to replace the outlier with its median:

replace_median <- function(x){
    quantiles <- quantile( x, c(0.25, 0.5, 0.75) )
    x[ x < quantiles[1] - 1.5*IQR(x) ] <- quantiles[2]
    x[ x > quantiles[3] + 1.5*IQR(x) ] <- quantiles[2]
    x
}

task2 <- anscombe1$y3 %>% replace_median()
```

---

# Transforming and binning values:

- Transforming variables can also eliminate outliers.

- Natural logarithm of a value reduces the variation caused by outliers.

- Binning is also a form of variable transformation.

- Transforming and binning will be covered in details in the next module.

---

# Outliers can also be valuable!

- We don’t always remove, impute, cap or transform suggested outliers in the data.

- For some applications, (i.e. in anomaly detection or fraud detection), outliers can provide valuable information or insight therefore analysts may chose to keep those values for further investigation.

- For such cases you may choose to leave (and investigate further) those values as they can tell you an interesting story about your data.

---

# Functions to Remember for Week 8

- `boxplot()`, `plot()`

- Outliers package `scores()`

- MVN package `mvn()`

- Practice!

---

# Class Worksheet

- Working in small groups, complete the following worksheet:

[Module 6 Worksheet](../worksheets/Week_08_Worksheet.html)

- Once completed, feel free to work on your Assessments.

[Return to Course Website](../index.html)